Actualidad informática
Noticias y novedades sobre informática
admin
Algoritmo para descubrir el origen de epidemias o el ataque a las Torres Gemelas
La fuente de un brote de cólera, el origen de un rumor en Facebook o el líder del grupo que echó abajo las Torres Gemelas pueden ser descubiertos con ecuaciones. En los tres casos existe una red en la que los pueblos infectados, los amigos de Facebook o los terroristas de Al Qaeda son los nodos y un flujo de información en forma de contagio, comentarios y comunicaciones. Teniendo controlados a unos pocos nodos de esas redes, un algoritmo puede determinar dónde o quién empezó todo.
Tres investigadores de la Ecole Polytechnique Fédérale de Lausanne (EPFL) han creado el algoritmo SparseInf con el que intentan inferir la localización de una fuente partiendo del control de unos pocos y dispersos (sparse, en inglés) nodos. Conociendo, al menos parcialmente, la topografía de una red compleja, el sentido de la circulación de la información y el momento en que los dos o tres nodos convertidos en sensor u observador la reciben, SparseInf llega al momento y fuente original con un alto grado de acierto.
Como los móviles
Pedro Pinto, principal autor del algoritmo y de la investigación que publica hoy la revista Physical Review Letters, explica su funcionamiento básico sin recurrir a complicadas ecuaciones matemáticas. ”El algoritmo es similar al sistema para la localización de los móviles. Si tu móvil se encuentra a 100 metros de la antena 1, a 200 metros de la antena 2 y 300 metros de la antena 3, podemos dibujar tres grandes círculos. El punto de intersección de los tres se corresponde con la ubicación de tu móvil, es lo que se llama triangulación”, explica. En SparseInf usan el mismo principio, pero aplicado a otro tipo de redes.
Artículo completo en: Materia
(cc) 2012, Materia Publicaciones Científicas S.L.
Para qué sirven las matemáticas
Peter Rowlett nos presenta en Nature siete ejemplos que demuestran que el trabajo teórico de los matemáticos puede conducir a aplicaciones prácticas inesperadas. Muchos científicos e ingenieros descubren que las herramientas matemáticas que necesitan fueron desarrolladas hace muchos años, incluso hace siglos, por matemáticos que no tenían en mente ninguna aplicación práctica concreta. La vida de las herramientas matemáticas, si no tienen errores, es eterna; una vez que la comunidad de matemáticos está satisfecha con una solución a cierto problema matemático, por dicha solución no pasan los años. Sin embargo, con la crisis económica ha crecido el interés en buscar aplicaciones a los desarrollos matemáticos en su etapa germinal, cuando aún son meras ideas abstractas. El problema es que para un matemático predecir para qué pueden servir sus ideas raya lo imposible. No se pueden forzar las cosas y algunas aplicaciones de las matemáticas actuales aparecerán dentro de décadas o incluso siglos. Para ilustrarlo, Peter Rowlett nos presenta los siguiente siete ejemplos en ”The unplanned impact of mathematics,” Nature 475: 166–169, 14 July 2011. La Sociedad Británica para la Historia de las Matemáticas tiene abierta una convocatoria con objeto de recopilar más ejemplos, si conoces alguno puedes enviarlo siguiendo este enlace “The British Society for the History of Mathematics.”
Los trabajos son:
Mark McCartney & Tony Mann: “De los cuaterniones a Lara Croft”
Graham Hoare: “De la geometría a la granexplosión”
Edmund Harris: “De las naranjas a los módems”
Juan Parrondo y Noel-Ann Bradshaw: “De una paradoja a las pandemias”
Peter Rowlett: “De los jugadores a las aseguradoras”
Julia Collins: “Desdeun puente hasta el ADN”
Chris Linton: “Desde las cuerdas a la energía nuclear”
Detalle de cada uno en: Francis (th)E mule Science’s News
Prueban matemáticamente que la Física es difícil
Científicos de la Universidad Complutense de Madrid (UCM) han demostrado matemáticamente que la Física es difícil. En el artículo ‘Es oficial: la Física es difícil, publicado por ‘Science’, los expertos han clasificado los problemas de acuerdo a su complejidad a través de la teoría matemática de la complejidad computacional permite.
Los científicos han señalado que en el colegio enseñan que la física intenta dar ecuaciones matemáticas que expliquen la evolución de un sistema en el tiempo a partir de observaciones del mismo. Posteriormente, con el auge actual de los supercomputadores uno podría esperar que este proceso se pudiera automatizar, sustituyendo la creatividad de los científicos por el poder de cálculo de los ordenadores. Sin embargo, los científicos de la UCM han demostrado matemáticamente que ésto no es posible.
Según destacan en el trabajo, hay problemas fáciles de resolver, como sumar o multiplicar dos números, y que por tanto se pueden automatizar y dejar que un ordenador los resuelva. Pero hay otros, como los problemas de optimización de la logística en el transporte de mercancías, que son muy difíciles. Tanto, que si hubiera una forma de automatizar su solución, se podría automatizar la solución de todos los problemas, algo que se cree imposible y que se conoce como la conjetura ‘P distinto de NP’.
Es precisamente a esta última clase de problemas muy difíciles a la que pertenece el problema de obtener las ecuaciones que rigen la evolución de los sistemas físicos.
En este sentido, los autores del estudio han señalado que su trabajo va a permitir «dormir tranquilo a todo el mundo». «A los físicos porque los supercomputadores no van a quitarles el trabajo y a los que no son físicos porque, aunque ya sospechaban que la física es difícil y por eso les costaba entenderla, ahora ya no hay duda: es una certeza matemática».
Nueva aplicación de IBM presenta cerca de 1000 años de historia de las Matemáticas
Nerds de las Matemáticas e historiadores, es el momento para emocionarse. Las mentes de la matemáticas moderna, una nueva aplicación para iPad publicada por IBM, que presenta una línea de tiempo interactiva de la historia de las matemáticas y su impacto en la sociedad desde 1000 hasta 1960.
La aplicación se basa en un original, 50 metros de largo «Los hombres de la Matemática Moderna», instalación creada en 1964 por Charles y Ray Eames. Las mentes de las matemáticas modernas se pueden ver una versión digitalizada de la infografía original, así como navegar a través de una línea de tiempo interactiva con más de 500 biografías, los hitos de matemáticase e imágenes de los artefactos pertinentes.
IBM espera que las clases y los estudiantes al utilizar la aplicación, provoque que más gente desee estudiar matemáticas, ciencia o educación relacionada con la tecnología .
«Las carreras del futuro dependerán en gran medida de la creatividad, el pensamiento crítico, resolución de problemas y la colaboración – todos los temas que fueron la base de las «Las Mentes de la Matemática Moderna» y siguen siendo igual de relevantes hoy en día,» dijo Chid Apte, Director de analytics Research and Mathematical Sciences en IBM , en un comunicado de prensa. «¿Qué mejor que una aplicación móvil para reintroducir este clásico atemporal para inspirar una nueva generación de estudiantes?»
A partir del primer papa francés al célebre matemático John von Neumann, los usuarios pueden ver todos los principales eventos relacionados con las matemáticas o la persona en un diseño visualmente impactante. Puede tocar en una entrada para leer más sobre esto, y ver cómo los eventos de matemáticas y las superestrellas de las matemáticas se relacionan en el tiempo con otros eventos históricos, como la primera cruzada que se apoderó deJerusalén y la firma de la Declaración de la Independencia.
Y en caso de quienes no han estudiado las matemáticas desde la escuela secundaria, la aplicación también incluye un «Peep Show IBM Matemáticas» de nueve clips animados de dos minutos que le ayudarán a repasar conceptos matemáticos, como la topología y los exponentes.
La aplicación se encuentra disponible de forma gratuita en la App Store. Pero si la versión para iPad no es suficiente, siempre puedes visitar la línea de tiempo a gran escala en exhibición en el New York Hall of Science en Queens, Nueva York y el Museo de la Ciencia, en Boston, MA.
Un sudoku necesita un mínimo de 17 cifras para tener una única solución
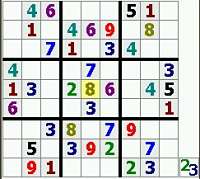El matemático de la Universidad de Dublín (Irlanda) Gary McGuire, ha utilizado un algoritmo complejo y «muchas horas de trabajo ante un superordenador» para determinar que un sudoku no se puede resolver si no hay un mínimo de 17 cifras-pista en su inicio, ya que con menos «no existe una solución única».
Este juego, que se hizo popular en Japón y es habitual en el espacio de pasatiempos, cuenta en su mayoría con unas 25 cifras-pista, según ha apuntado el científico. A medida que bajan las pistas, más difícil es su resolución.
La complejidad del sudoku ha llevado a los matemáticos a estudiarlo. Ahora, McGuire ha llegado a esta conclusión tras trabajar durante dos años en el algoritmo complejo que le ha llevado a la solución.
«La única manera realista de conseguir resultados era el método de la fuerza bruta», ha apuntado McGuire, quien ha añadido que «su investigación ha inspirado para impulsar las técnicas de computación y matemáticas hasta el límite».
McGuire ha simplificado el trabajo de algunos de sus compañeros, que le han precedido en esta investigación, mediante el diseño de un algoritmo que evitara lo que el científico ha denominado «series inevitables» o «lo que podría dar lugar a múltiples soluciones».
Según ha señalado la revista ‘Nature’, el anuncio de este hallazgo se ha producido en un cogreso matemático celebrado en Boston (Estados Unidos) el pasado siete de enero y en donde recibió la aprobación de sus compañeros. «El enfoque es razonable y es plausible», ha apuntado el matemático de la Universidad James Madison (Estados Unidos).
Fuente: LAVANGUARDIA.com CIENCIA
2012: El año de Alan Turing
Ayudó a ganar la Segunda Guerra Mundial al descifrar el código alemán Enigma, pero fue perseguido por Gran Bretaña por ser gay. Hoy, su nombre es sinónimo de la prueba de que inventó en 1950 para determinar la capacidad de una máquina para tener un comportamiento inteligente. http://www.loebner.net/Prizef/TuringArticle.html
El 23 de junio 2012 será el centenario del nacimiento de Alan Turing, y una celebración del centenario se ha planificado con actividades en todo el mundo. Es quizás lo más apropiado que Royal Mail emitirá un sello conmemorativo, un homenaje póstumo a uno de los héroes de Inglaterra, que fue tan maltratado durante su vida. http://www.mathcomp.leeds.ac.uk/turing2012/give-page.php?13
El Año de Turing también presenta un marco interesante para nosotros, para medir el progreso de la informática. Cuando Turing inventó su prueba en 1950, algunos predijeron que la llamada «Inteligencia Artificial fuerte», es decir, la inteligencia artificial que iguala o supera la inteligencia humana, se podría lograr en unas pocas décadas. Más de sesenta años después, cada máquina que se ha encargado de simular la inteligencia humana no ha pasado la prueba llamada Turing.
Y, sin embargo, los científicos han llegado a impresionarse y alarmarse por los saltos hacia adelante de las capacidades de la Inteligencia Artificial en los últimos años. Se ha usado de forma habitual por las instituciones financieras, y se encontraron aplicaciones prometedoras en equipos médicos, la tecnología de búsqueda, juegos y sistemas de transporte. Por otro lado, los avances se han realizado en creaciones aparentemente Frankenstein tales como virus informáticos y depredadores.
La informática se asocia con el dinero y no con la ciencia
Donald E. Knuth, matemático estadounidense, ha ganado, a sus 73 años, el premio Fronteras del Conocimiento por “hacer de la programación informática una ciencia”
El matemático Donald Knuth (Wisconsin, EEUU, 1938) está entusiasmado con su visita a Madrid, pero no sólo por haber ganado el premio Fronteras del Conocimiento en Tecnologías de la Información y la Comunicación de la Fundación BBVA dotado con 400 000 euros, sino porque, al día siguiente de su llegada a España, tuvo la oportunidad de tocar el órgano del Palacio Real, una de las aficiones de este hombre polifacético que, sin embargo, sabe bien cuál es su mejor talento: “Escribir buenos libros sobre ordenadores. Si termino de escribir mi obra antes de volverme senil, haré música, pero lo primero sé que lo hago muy bien, mientras que mi música puede que sea horrible”, bromea. Knuth es autor de El arte de programar ordenadores que, según el jurado del premio, es “el trabajo más relevante de la ingeniería informática, en su sentido más amplio. Su impacto, tanto en la teoría como en la práctica, no tiene parangón”, añade el acta. Empezó a trabajar en esta obra en 1962 y sigue completándola.
Una de las razones por las que le han premiado es por convertir la programación en ciencia. ¿Siente que la informática está igual de valorada que otras disciplinas más clásicas?
Sí. De hecho, llegamos a este nivel hace ya 20 o 30 años, pero después tuvimos tanto éxito que la gente se dio cuenta de que la computación respondía a preguntas realmente interesantes y difíciles. Esto ha hecho que, para mucha gente, esté más asociada al dinero que a la ciencia. Para medir el éxito de un programador, las personas se preguntan ¿cuántas empresas tiene? ¿Será un millonario como Bill Gates?
¿Por qué empezó a programar con código abierto?
Es sencillo. Si tenemos a mucha gente trabajando en una idea, será más fácil saber por qué algo no funciona y encontrar una solución. Si yo uso un programa de Microsoft y no me funciona, lo único que haré será enfadarme más y más. Yo empecé a trabajar en código abierto porque me ganaba la vida como científico y programar era una de mis tareas. Si hacía accesible mi trabajo a todo el mundo, tendría a miles de personas ayudándome. Si lo hacía en privado, sin embargo, mi trabajo no se extendería.
Ampliar información en: Público.es
Foto: Wikipedia en portugués.
__________________________
Enlaces de interés:
– Apuntes Informática Aplicada al Trabajo Social. Capitulo 5 Aplicaciones software
Superordenador IBM para calcular dígitos de Pi
Investigadores australianos han hecho lo imposible, han encontrado el sesenta billonésimo dígito binario de Pi-cuadrado. El cálculo si se hubiera realizado en una computadora con solo una CPU, habría llevado 1500 años, pero los científicos de IBM y la Universidad de Newcastle lograron completar este trabajo en tan sólo unos meses con el superordenador de IBM «Blue Gene / P», que está diseñado para realizar un cuatrillón de cálculos por segundo.
Su trabajo se basó en una fórmula matemática descubierta hace una década, en parte en el Department of Energy’s, por David H. Bailey Jefe de Tecnología del Departamento de Investigación Computacional en Lawrence Berkeley National Laboratory. El equipo australiano tomó el programa de Bailey, que se desarrolló para un equipo PC de procesador únic PC, y lo hizo correr más rápido y en paralelo, en miles de procesadores independientes.
«Lo que es interesante en estos cálculos es que hasta hace pocos años, se creía ampliamente que tales objetos matemáticos estarían siempre fuera del alcance del razonamiento humano o de las máquina de cómputación», dijo Bailey. «Una vez más vemos la inutilidad absoluta de poner límites en el ingenio humano y la tecnología.»
Un «bit» o dígito binario es el «ADN» de cada computadora. En un equipo, todo se representa como cadenas de ceros y unos. El número decimal 12, por ejemplo, se representa como «1100», y la fracción 9.16 se representa como «.1001.» Así como uno puede imaginar, el cálculo del sesenta billonésimo dígito binario de un número es toda una hazaña.
Según el profesor Jonathan Borwein de la Universidad de Newcastle, este trabajo representa el cálculo más grande hecho de cualquier objeto matemático hasta la fecha. La idea de este proyecto se desencadenó cuando IBM Australia estaba buscando algo que hacer relacionado con el «Día Pi» (14 de marzo) en un nuevo sistema informático IBM BlueGene / P . Borwein propuso ejecutar fórmula de Bailey de Pi-cuadrado. El equipo también calcula la constante de catalán, otro número importante que se plantea en las matemáticas.
¿Por qué Pi?
La importancia de Pi se sabe desde hace tiempo – se multiplica por el diámetro de un círculo para obtener la circunferencia. Los antiguos egipcios ba este número en el diseño de las pirámides, por su parte autores de la antigüedad en Jerusalén, India, Babilonia, Grecia y China utilizaron esta proporción en sus estudios de arquitectura y símbolos.
Sin embargo, a pesar de su longevidad, Pi es uno de los números más misteriosos de las matemáticas. Debido a que es «irracional», Pi no puede ser expresado como un número decimal finito y la humanidad no tendrá nada más que aproximaciones del mismo. Así que ¿por qué molestarse en resolver Pi con tantos decimales? Después de todo, un valor de Pi con 40 dígitos sería más que suficiente para calcular la circunferencia de la Vía Láctea con un error menor que el tamaño de un protón.
Según Bailey, una aplicación para el cálculo de los dígitos de Pi es poner a prueba la integridad de hardware y software, que es un foco de la investigación de Bailey en el Berkeley Lab. «Si dos cálculos separados de dígitos de Pi, por ejemplo utilizando algoritmos distintos, están de acuerdo, excepto quizás por unos pocos dígitos al final, entonces casi seguro que ambos equipos realizan billones de operaciones sin problemas», dice.
Por ejemplo, en 1986, un programa de cálculo de Pi-que Bailey escribió en la NASA, mediante un algoritmo de Jonathan y Peter Borwein, detectó algunos problemas de hardware en uno de los primeros superordenadores Cray-2 que había escapado de las pruebas del fabricante. En esta misma línea, algunas técnicas de mejora para el cálculo de lo que se conoce como la transformada rápida de Fourier en los sistemas informáticos modernos tienen sus raíces en los esfuerzos para acelerar los cálculos de Pi. Estas técnicas mejoradas son ahora ampliamente utilizadas en aplicaciones científicas y de ingeniería. Y, por supuesto, desde una perspectiva matemática es simplemente fascinante ver los dígitos de Pi en acción!
Más información: lSeeer más acerca de Pi en el blog de Bailey . Y encontrar más información sobre el Laboratorio de Ciencias de la Computación de Berkeley aquí .
autobus las palmas aeropuerto cetona de frambuesa