Actualidad informática

En otro artículo os contaba la historia de María Estuardo, de cómo utilizó el cifrado de sustitución y cómo la cogieron porque el criptoanalista, Thomas Phelippes, conocía los métodos estadísticos necesarios para descifrar sus mensajes. Hoy daremos un paso más en lo que al cifrado de mensajes se refiere y que culminará en la máquina de codificación más temible y famosa de la Segunda Guerra Mundial: la máquina Enigma.

Primero, no obstante, he de explicaros el cifrado de Vigenère. Básicamente consiste en un cifrado de sustitución, como el citado anteriormente del artículo de María Estuardo, pero  diferente para cada letra en función de una clave. No os asustéis: vayamos por partes. Os muestro a continuación la tabla de Vigenère:

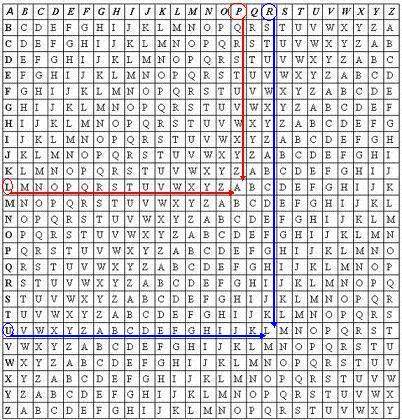
Es una tabla con los alfabetos empezando cada vez por una letra posterior. La mejor forma de ver cómo funciona es explicando un ejemplo. Seguiré el mismo de la Wikipedia.

mensaje:         P A R I S   V A U T  B I E N   U N E  M E S S E
clave:              L O U P L  O U P L  O U P L  O U P  L O U P L
criptograma:   A O L X D   J U J E   P C T Y  I H T   X S M H P

La clave es LOUP y así se va repitiendo letra tras letra. Vamos a codificar la primera P. Tomamos dicha P (del texto) de la primera fila y la L (de la clave) de la primera columna. Vemos que se cortan en la A y esa es la primera letra cifrada (está destacado en rojo en el gráfico anterior). Ahora vamos a cifrar la A. Análogamente, tomamos la A de la primera fila y la O de la primera columna: tenemos la O. Para la R, la tomamos también de la primera fila y la U de la primera columna y vemos que se cruzan en la L (destacado en azul en el gráfico anterior). Y así sucesivamente.

Si alguien intercepta el mensaje y no conoce la clave no podrá descifrarlo  a priori sin conocer la clave; aunque sepa que es una codificación de Vigenère. Los métodos estadísticos no sirven, ya que la misma letra puede ser codificada de formas diferentes. A primera vista, parece imposible de descifrar, pero los criptoanalistas son gente muy hábil. Y lo consiguieron. Resulta que si conocemos la longitud de la clave ya podemos atacar el problema. Supongamos, como en este caso, que sabemos que la longitud de la clave es 4 (LOUP). Lo único que hay que hacer es un análisis estadístico para las posiciones 1, 5, 9, …; otro para 2, 6, 10, …; otro para 3, 7, 11, …; y finalmente otro para 4, 8, 12, … ya que el cifrado se repite cada cuatro posiciones y, por tanto, cada cuatro posiciones, tenemos una sustitución simple resoluble con los métodos estadísticos.

Para averiguar la longitud podemos hacerlo a través de la búsqueda de repeticiones en el texto (requiere una explicación, y la encontraréis en el libro que cito en fuentes). Recordad que siempre estamos pensando en un texto suficientemente largo. Ya podéis intuir que el secreto de la cifra Vigenère está en el tamaño de la clave: a clave más larga, mayor dificultad.

Esta codificación es obra, obviamente, de Blaise de Vigenère y estoy hablando de allá por el año 1585.

Artículo completo en: Historias de la Ciencia

Bajo licencia Creative Commons