Actualidad informática
Noticias y novedades sobre informática
admin
El problema del viajante
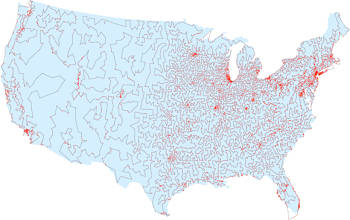
El problema del viajante consiste en encontrar el camino más corto que permite visitar una serie de ciudades conectadas por carreteras volviendo al punto de partida y visitando cada ciudad una sola vez. No hay ningún algoritmo eficiente para resolver este problema (que es NP-duro) . En 1950 los ordenadores permitían resolver un problema con 50 ciudades, en 1980 con unas 2300 ciudades y en 2006 se alcanzó el récord actual, 85900 ciudades (en la figura aparecen 13509 ciudades de EEUU). Los informáticos han tratado de descubrir algoritmos eficientes que aproximen la solución del problema. En 1976, Nicos Christofides (Imperial College, Londres) desarrolló un algoritmo eficiente que produce caminos cuyo coste excede al óptimo en menos del 50%. ¿Se puede mejorar? En 2011, se logró mejorar el algoritmo de Christofides con un nuevo algoritmo eficiente que excede del óptimo en menos del 49,99999999999999999999999999999999999999999999999996 por ciento. ¿Por qué ha costado tanto obtener una ventaja tan pequeña? Nadie lo sabe, pero resulta muy sugerente. Nos lo cuenta Erica Klarreich, “Computer Scientists Take Road Less Traveled. After decades without progress, new shortcuts are discovered in the traveling salesman problem,” Simons Foundation, Jan 29, 2013.
Fuente: Francis (th)E mule Science’s News
Algoritmo para descubrir el origen de epidemias o el ataque a las Torres Gemelas
La fuente de un brote de cólera, el origen de un rumor en Facebook o el líder del grupo que echó abajo las Torres Gemelas pueden ser descubiertos con ecuaciones. En los tres casos existe una red en la que los pueblos infectados, los amigos de Facebook o los terroristas de Al Qaeda son los nodos y un flujo de información en forma de contagio, comentarios y comunicaciones. Teniendo controlados a unos pocos nodos de esas redes, un algoritmo puede determinar dónde o quién empezó todo.
Tres investigadores de la Ecole Polytechnique Fédérale de Lausanne (EPFL) han creado el algoritmo SparseInf con el que intentan inferir la localización de una fuente partiendo del control de unos pocos y dispersos (sparse, en inglés) nodos. Conociendo, al menos parcialmente, la topografía de una red compleja, el sentido de la circulación de la información y el momento en que los dos o tres nodos convertidos en sensor u observador la reciben, SparseInf llega al momento y fuente original con un alto grado de acierto.
Como los móviles
Pedro Pinto, principal autor del algoritmo y de la investigación que publica hoy la revista Physical Review Letters, explica su funcionamiento básico sin recurrir a complicadas ecuaciones matemáticas. ”El algoritmo es similar al sistema para la localización de los móviles. Si tu móvil se encuentra a 100 metros de la antena 1, a 200 metros de la antena 2 y 300 metros de la antena 3, podemos dibujar tres grandes círculos. El punto de intersección de los tres se corresponde con la ubicación de tu móvil, es lo que se llama triangulación”, explica. En SparseInf usan el mismo principio, pero aplicado a otro tipo de redes.
Artículo completo en: Materia
(cc) 2012, Materia Publicaciones Científicas S.L.
Un sudoku necesita un mínimo de 17 cifras para tener una única solución
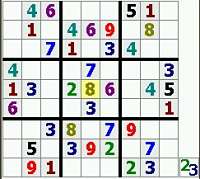El matemático de la Universidad de Dublín (Irlanda) Gary McGuire, ha utilizado un algoritmo complejo y «muchas horas de trabajo ante un superordenador» para determinar que un sudoku no se puede resolver si no hay un mínimo de 17 cifras-pista en su inicio, ya que con menos «no existe una solución única».
Este juego, que se hizo popular en Japón y es habitual en el espacio de pasatiempos, cuenta en su mayoría con unas 25 cifras-pista, según ha apuntado el científico. A medida que bajan las pistas, más difícil es su resolución.
La complejidad del sudoku ha llevado a los matemáticos a estudiarlo. Ahora, McGuire ha llegado a esta conclusión tras trabajar durante dos años en el algoritmo complejo que le ha llevado a la solución.
«La única manera realista de conseguir resultados era el método de la fuerza bruta», ha apuntado McGuire, quien ha añadido que «su investigación ha inspirado para impulsar las técnicas de computación y matemáticas hasta el límite».
McGuire ha simplificado el trabajo de algunos de sus compañeros, que le han precedido en esta investigación, mediante el diseño de un algoritmo que evitara lo que el científico ha denominado «series inevitables» o «lo que podría dar lugar a múltiples soluciones».
Según ha señalado la revista ‘Nature’, el anuncio de este hallazgo se ha producido en un cogreso matemático celebrado en Boston (Estados Unidos) el pasado siete de enero y en donde recibió la aprobación de sus compañeros. «El enfoque es razonable y es plausible», ha apuntado el matemático de la Universidad James Madison (Estados Unidos).
Fuente: LAVANGUARDIA.com CIENCIA
autobus las palmas aeropuerto cetona de frambuesa