Actualidad informática
Noticias y novedades sobre informática
¿Para qué se necesita una teoría cuántica de la gravedad? Para evitar los viajes cuánticos al pasado
La teoría de la gravedad de Einstein no prohíbe viajar en el tiempo hacia el pasado (curvas temporales cerradas). En sistemas macroscópicos parece imposible y se asume la existencia de principios (”censores cósmicos”) que evitan su existencia (básicamente que nada puede superar la velocidad de la luz). Sin embargo, cuando se unen la mecánica cuántica y la teoría de la gravedad la cosa cambia y no sabemos cómo evitar que un estado cuántico viaje al pasado. ¿Algún problema? Bueno, si fuera posible, los sistemas de cifrado cuántico, supuestamente absolutamente seguros, no lo serían, como nos cuenta David Lindley en “Time Travel Beats Quantum Mechanics,” Physical Review Focus, 2 June 2009, haciéndose eco del artículo técnico de Todd A. Brun, Jim Harrington, Mark M. Wilde, “Localized Closed Timelike Curves Can Perfectly Distinguish Quantum States,” Physical Review Letters 102: 210402, 2009 (ArXiv preprint). La existencia de curvas temporales cerradas (”closed timelike curves”, CTCs) en un contexto cuántico no es un problema para la mayoría de los investigadores ya que se cree que la teoría “correcta” de la gravedad cuántica evitará la existencia de este tipo de “inconsistencias” en nuestro conocimiento actual. Pero realmente será así. Todavía, nadie lo sabe.
Dibujo20090807_circuit_using_closed_timelike_curvesEl trabajo de Todd Brun et al. muestra que un espía podría utilizar curvas temporales cerradas (CTCs) para descifrar “al vuelo” los mensajes codificados utilizando cualquier sistema de criptografía cuántica sin que ni el emisor ni el receptor se dieran cuenta. La paradoja del abuelo, viajas al pasado y matas a tu abuelo, parece que prohíbe terminantemente la existencia de CTCs. Desde el punto de vista clásico todo el mundo lo tiene muy claro. Pero en 1991, David Deutsch de la Universidad de Oxford, Gran Bretaña, publicó un artículo en el que demostraba que las curvas temporales cerradas para ciertos estados cuánticos pueden evitar esta paradoja. Más aún, utilizando técnicas de teoría cuántica de la computación demostró que estas paradojas no pueden darse en un contexto cuántico. Ello no quita que las CTCs tengan otro tipo de ”defectos” cuánticos, como violaciones de la unitariedad y del principio de correspondencia, pero que nos parecen menos “antiintuitivos.” Además, también son computacionalmente interesantes, permitiendo, por ejemplo, la clonación de estados cuánticos. El artículo técnico es David Deutsch, “Quantum mechanics near closed timelike lines,” Phys. Rev. D 44: 3197-3217, 1991.
Sin entrar en detalles técnicos, lo más importante es que este trabajo apunta a la necesidad de una teoría cuántica de la gravedad en un contexto práctico (ya hay sistemas de cifrado cuántico comerciales) muy diferente al razonamiento habitual que requiere dicha teoría sólo para entender las singularidades ocultas en los agujeros negros o los primeros estadios de la Gran Explosión en cosmología teórica, muy alejados de lo experimentalmente verificable en laboratorio.
Fuente: Francis (th)E mule Science’s News
__________________
Enlaces relacionados:
– Tutoriales y divulgación de Física
La máquina Enigma
En otro artículo os contaba la historia de María Estuardo, de cómo utilizó el cifrado de sustitución y cómo la cogieron porque el criptoanalista, Thomas Phelippes, conocía los métodos estadísticos necesarios para descifrar sus mensajes. Hoy daremos un paso más en lo que al cifrado de mensajes se refiere y que culminará en la máquina de codificación más temible y famosa de la Segunda Guerra Mundial: la máquina Enigma.
Primero, no obstante, he de explicaros el cifrado de Vigenère. Básicamente consiste en un cifrado de sustitución, como el citado anteriormente del artículo de María Estuardo, pero diferente para cada letra en función de una clave. No os asustéis: vayamos por partes. Os muestro a continuación la tabla de Vigenère:
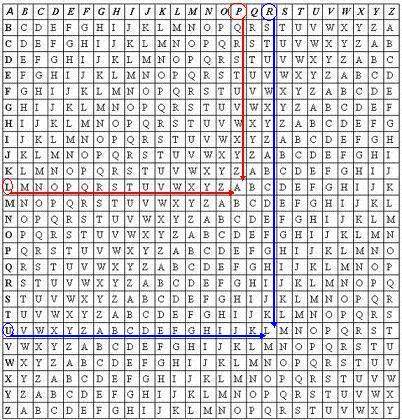
Es una tabla con los alfabetos empezando cada vez por una letra posterior. La mejor forma de ver cómo funciona es explicando un ejemplo. Seguiré el mismo de la Wikipedia.
mensaje: P A R I S V A U T B I E N U N E M E S S E
clave: L O U P L O U P L O U P L O U P L O U P L
criptograma: A O L X D J U J E P C T Y I H T X S M H P
La clave es LOUP y así se va repitiendo letra tras letra. Vamos a codificar la primera P. Tomamos dicha P (del texto) de la primera fila y la L (de la clave) de la primera columna. Vemos que se cortan en la A y esa es la primera letra cifrada (está destacado en rojo en el gráfico anterior). Ahora vamos a cifrar la A. Análogamente, tomamos la A de la primera fila y la O de la primera columna: tenemos la O. Para la R, la tomamos también de la primera fila y la U de la primera columna y vemos que se cruzan en la L (destacado en azul en el gráfico anterior). Y así sucesivamente.
Si alguien intercepta el mensaje y no conoce la clave no podrá descifrarlo a priori sin conocer la clave; aunque sepa que es una codificación de Vigenère. Los métodos estadísticos no sirven, ya que la misma letra puede ser codificada de formas diferentes. A primera vista, parece imposible de descifrar, pero los criptoanalistas son gente muy hábil. Y lo consiguieron. Resulta que si conocemos la longitud de la clave ya podemos atacar el problema. Supongamos, como en este caso, que sabemos que la longitud de la clave es 4 (LOUP). Lo único que hay que hacer es un análisis estadístico para las posiciones 1, 5, 9, …; otro para 2, 6, 10, …; otro para 3, 7, 11, …; y finalmente otro para 4, 8, 12, … ya que el cifrado se repite cada cuatro posiciones y, por tanto, cada cuatro posiciones, tenemos una sustitución simple resoluble con los métodos estadísticos.
Para averiguar la longitud podemos hacerlo a través de la búsqueda de repeticiones en el texto (requiere una explicación, y la encontraréis en el libro que cito en fuentes). Recordad que siempre estamos pensando en un texto suficientemente largo. Ya podéis intuir que el secreto de la cifra Vigenère está en el tamaño de la clave: a clave más larga, mayor dificultad.
Esta codificación es obra, obviamente, de Blaise de Vigenère y estoy hablando de allá por el año 1585.
Artículo completo en: Historias de la Ciencia
Bajo licencia Creative Commons

autobus las palmas aeropuerto cetona de frambuesa