Actualidad informática

En el estudio, los físicos Joan Vaccaro de la Universidad Griffith de Queensland, Australia, y Stephen Barnett, de la Universidad de Strathclyde en Glasgow, Reino Unido, han descrito cómo la información cuantitativa se pueden borrar sin consumo de ningún tipo de energía.  Su trabajo se ha  publicado en una edición reciente de Proceedings of the Royal Society A.

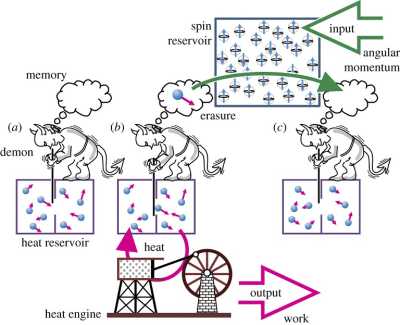
El demonio de Maxwell puede extraer trabajo de un solo reservorio de calor a costo de momento angular de espín. En el paso (a), el demonio no tiene memoria y el gas en el reservorio de calor está en equilibrio térmico. En el paso (b), el demonio divide el reservorio en dos, atrapando las moléculas de mayor movimiento en el lado derecho, y utiliza un ingenio de calor entre las dos particiones para obtener trabajo. En el paso (c), la memoria del demonio se borra usando un reservorio de espín y a las dos particiones se les permite regresar al equilibrio. Crédito de la imagen: Joan A. Vaccaro, et al. Fig. 1. © 2011 Royal Society.

Tradicionalmente, el proceso de borrado de información requiere de un costo que se calcula en términos de energía – disipación de calor más concretamente. En 1961, Rolf Landauer argumentó que había una cantidad mínima de energía necesaria para borrar un bit de información, es decir, poner un bit en el estado lógico cero. La energía necesaria se relaciona positivamente con la temperatura del reservorio  del sistema térmico, y puede considerarse como la entropía termodinámica del sistema. Como tal, esta entropía se considera un costo fundamental para borrar un bit de información.

Sin embargo, Vaccaro y Barnett han demostrado que un gasto de energía puede ser totalmente evitado mediante el uso de un depósito basado en algo distinto de la energía, tal como momento angular de espín. Las partículas subatómicas tienen momento angular de espín, una cantidad que, como la energía, debe ser conservado. Básicamente, en vez de calor que se intercambia entre un qubit y  el reservorio térmico, cuantos discretos de momento angular se intercambian entre un qubit y el reservorio de espín. Los científicos describen cómo repetidas operaciones lógicas entre el espín del qubit y un espín secundario en el estado cero eventualmente da lugar a que ambos espines alcancen el estado lógico cero. Más importante aún, los científicos demostraron que el costo de borrar la memoria del qubit se da en términos de la cantidad que define los estados lógicos, que en este caso es el  momento angular de espín y no la energía.

Los científicos explicaron que experimentalmente la realización de este esquema sería muy difícil. Sin embargo, sus resultados muestran que las leyes físicas no impiden borrar la información con un coste energético cero, lo que es contrario a los estudios anteriores. Los investigadores observaron que, en la práctica, será especialmente difícil garantizar la degeneración del sistema de energía (que los diferentes estados de espín del qubit y el reservorio tienen exactamente el nivel de  energía). Pero incluso si las condiciones son imperfectas y causan la pérdida de energía, no hay razón fundamental para asumir que el costo será mayor que lo predicho por la fórmula de Landauer.

La posibilidad de borrar la información sin necesidad de utilizar la energía tiene implicaciones para diversas áreas. Un ejemplo es la paradoja del demonio de Maxwell, que parece ofrecer una forma de violar la segunda ley de la termodinámica. Al abrir y cerrar una puerta para separar las moléculas calientes y frías, el demonio supuestamente extrae trabajo del depósito, la conversión de todo el calor en energía mecánica útil. La resolución de Bennett de la paradoja en 1982 sostiene que la memoria del demonio tiene que ser borrada para completar el ciclo, y el costo de eliminación es por lo menos tanto como la energía liberada. Sin embargo, los resultados de Vaccaro y Barnett sugiere que la memoria del demonio se pueden borrar sin costo de energía mediante el uso de otro tipo de depósito, donde el costo sería en términos del momento angular de espín. En este esquema, el demonio puede extraer toda la energía de una reserva de calor como energía útil a un costo de otro recurso.

Como explicaron los científicos, este resultado no se contradice con las afirmaciones históricas de la segunda ley de la termodinámica, que están exclusivamente en el contexto de reservorios de calor y térmicos, y no permiten una clase más amplia de reservorios. Por otra parte, a pesar de que el ejemplo con el demonio de Maxwell sugiere que el trabajo mecánico se puede extraer a un costo cero de energía, esta extracción se asocia con un aumento en la entropía de la información teórica del sistema en general.

«La maximización de la entropía sujeta a una restricción es necesario aplicar no sólo para calentar los reservorios y la conservación de la energía», explicó Vaccaro a PhysOrg.com.

Los resultados también podrían aplicarse a hipotéticos motores de calor de Carnot, que operan con la máxima eficacia. Si estos motores utilizan depósitos de momento angular en lugar de depósitos térmicos,  podrían generar  esfuerzos de momento angular en lugar de trabajo mecánico.

Para demostrar el concepto de borrar información a un coste energético cero, los científicos dijeron que se necesitarían más investigaciones y tiempo.

Añadió que el resultado es de importancia fundamental, y no es probable que tenga aplicaciones prácticas para dispositivos de memoria. «No vemos esto como que tenga un impacto directo en términos de aplicaciones prácticas, ya que el coste energético actual de la supresión de información está próximo al teórico de Landauer «, dijo. «Es más un caso de lo que dice acerca de conceptos fundamentales. Por ejemplo, Landauer, dijo que la información es física, porque se necesita energía para borrarla. Estamos diciendo que la razón es física, tiene un contexto más amplio que eso. »

AMpliar información en: Joan A. Vaccaro and Stephen M. Barnett. “Information erasure without an energy cost.” Proceedings of the Royal Society A.DOI:10.1098/rspa.2010.0577